I/O Performance for Versioned-HDF5 Files

For these tests, we have generated .h5 data files using the generate_data.py script from the VersionedHDF5 repository, using the standard options (see more details in Performance.)

We performed the following tests:

1. Test Large Fraction Changes Sparse

2. Test Mostly Appends Sparse

3. Test Small Fraction Changes Sparse

4. Test Large Fraction Changes (Constant Array Size) Sparse

5. Test Mostly Appends Dense

The .h5 files used in these tests should be generated separately, using the performance_tests.py script from analysis folder.

Setup

import h5py
import json
import time
import numpy as np
import performance_tests
import matplotlib.pyplot as plt
from versioned_hdf5 import VersionedHDF5File

Test 1: Large fraction changes (sparse)

testname = "test_large_fraction_changes_sparse"

Reading in sequential mode

For this test, we’ll read data from all versions in a file, sequentially.

def read_times(filename):
    h5pyfile = h5py.File(filename, 'r+')
    vfile = VersionedHDF5File(h5pyfile)
    t0 = time.time()
    for vname in vfile._versions:
        if vname != '__first_version__':
            version = vfile[vname]
            group_key = list(version.keys())[0]
            val = version[group_key]['val']
    t = time.time()-t0
    h5pyfile.close()
    vfile.close()
    return t

To keep this test short, we’ll only analyze the tests using no compression, and chunk size \(2^{14}\). Note that this can be changed in the lines below if desired.

compression = "None"
exponent = 14

Plotting with respect to the number of versions, we get the following:

rtimes = []
num_transactions = [50, 100, 500, 1000, 5000]
for n in num_transactions:
    filename = f"{testname}_{n}_{exponent}_{compression}.h5"
    rtimes.append(read_times(filename))

fig = plt.figure(figsize=(10,6))

plt.plot(num_transactions, rtimes, 'o-')
selected = [0, 2, 3, 4]
plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Sequential read time (in sec) for {testname}")
plt.xlabel("Number of transactions")
plt.show()

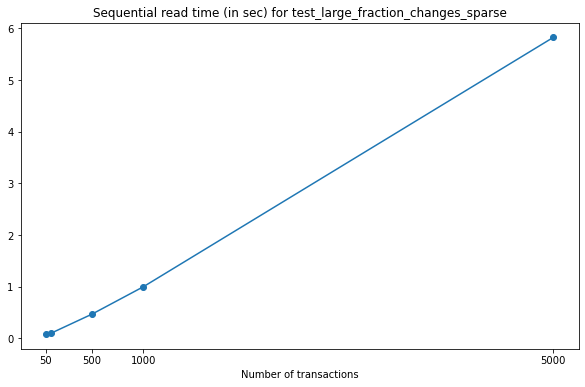
As expected, read times increase for files with a larger number of versions, but the growth is close to linear.

Reading specific version

For this test, we’ll compute the times required to read a specific version from the versioned-hdf5 file.

Note. Although possible, it is not recommended to read versions using integer indexing as the performance of reading versions from their name it far superior.

In the code below you can choose to read a random version from the file, or the version which is approximately at half of the version set (for reproducibility reasons).

def read_version(filename, n):
    h5pyfile = h5py.File(filename, 'r+')
    vfile = VersionedHDF5File(h5pyfile)
    # If you want to choose a version at random,
    # N = len(vfile._versions.keys())
    # index = np.random.randint(0, N)
    index = n // 2
    vname = list(vfile._versions.keys())[index]
    t0 = time.time()
    version = vfile[vname]
    # It is not recommended to use integer indexing for
    # performance reasons:
    # e.g. version = vfile[-index]
    # This is much slower than reading from a version name.
    group_key = list(version.keys())[0]
    val = version[group_key]['val']
    t = time.time()-t0
    h5pyfile.close()
    vfile.close()
    return t

The next plot contains a set of 20 reads for the middle element of each file (each line in the figure represents a run). It is expected that there are variations in the read times, as this fluctuates with the system load while running the test.

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10, 6))

for _ in range(20):
    vtimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        vtimes.append(read_version(filename, n))
    plt.plot(num_transactions, vtimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read specific version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

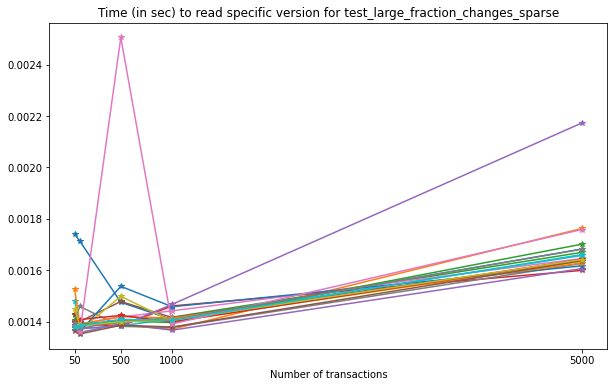
From this test, we can see that reading an arbitrary version from the file is very slightly affected by the number of versions in the file.

Reading first version vs. reading latest version

Next, we’ll compare the times necessary to read the first version and the latest version on each file.

def read_first(filename):
    h5pyfile = h5py.File(filename, 'r+')
    vfile = VersionedHDF5File(h5pyfile)
    t0 = time.time()
    version = vfile['initial_version']
    group_key = list(version.keys())[0]
    val = version[group_key]['val']
    t = time.time()-t0
    h5pyfile.close()
    vfile.close()
    return t

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10, 6))

for _ in range(20):
    ftimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ftimes.append(read_first(filename))
    plt.plot(num_transactions, ftimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read first version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

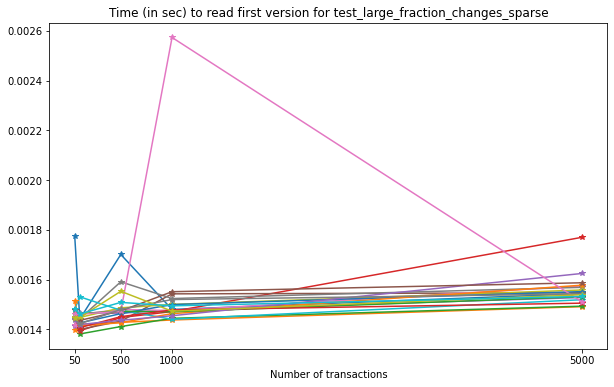
Note that, on average, the time required to read the contents of the first version written to the file do not increase significantly with the number of versions stored in the file.

The Versioned HDF5 file stores the latest version as the last to be stored in the file. For comparison, we will also measure reading times for files generated without versioning (i.e. with no use of Versioned HDF5). Note that these should be similar data.

def read_last(filename):
    h5pyfile = h5py.File(filename, 'r+')
    vfile = VersionedHDF5File(h5pyfile)
    t0 = time.time()
    #
    # Current version is 0
    # This is the same as
    # version = vfile[vfile._versions.attrs['current_version']]
    #
    version = vfile[0]
    group_key = list(version.keys())[0]
    val = version[group_key]['val']
    t = time.time()-t0
    h5pyfile.close()
    vfile.close()
    return t

def read_no_versions(filename):
    h5pyfile = h5py.File(filename, 'r+')
    t0 = time.time()
    val = h5pyfile[list(h5pyfile.keys())[0]]['val']
    t = time.time()-t0
    h5pyfile.close()
    return t

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

# We only do one run for the unversioned files.
notimes = []
for i in range(5):
    n = num_transactions[i]
    filename = f"{testname}_{n}_{exponent}_{compression}_no_versions.h5"
    notimes.append(read_no_versions(filename))
plt.plot(num_transactions, notimes, 'ko-', ms=6)
plt.legend(["No versions"], loc="upper left")

for _ in range(20):
    ltimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ltimes.append(read_last(filename))
    plt.plot(num_transactions, ltimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read latest version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

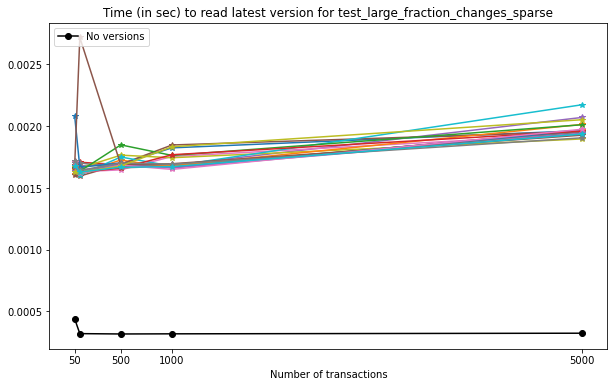
In this case, we can see that:

• on average, reading the latest version on a VersionedHDF5File is ~5x slower than reading an unversioned file;

• the time required to read the latest version from a Versioned HDF5 file increases modestly with the number of versions stored in the file.

Test 2: Mostly appends (Sparse)

testname = "test_mostly_appends_sparse"

Once again, for shortness, we’ll only consider

compression = "None"
exponent = 14

Reading in sequential mode

If we read data from each version of the file, sequentially, we obtain the following:

rtimes = []
num_transactions = [25, 50, 100, 500]
for n in num_transactions:
    filename = f"{testname}_{n}_{exponent}_{compression}.h5"
    rtimes.append(read_times(filename))

fig = plt.figure(figsize=(10,6))

plt.plot(num_transactions, rtimes, 'o-')
selected = [0, 1, 2, 3]
plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Sequential read time (in sec) for {testname}")
plt.xlabel("Number of transactions")
plt.show()

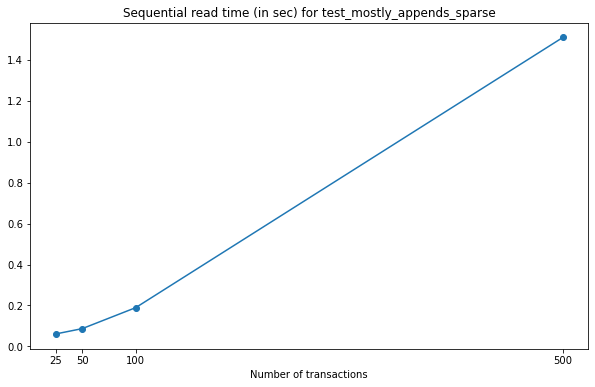
In this case, we can see that the increase in the time required to read the datasets from the VersionedHDF5File grows quadratically with the number of transactions stored in the file. This is consistent with the increase in the size of the dataset, which also grows quickly with each new version commited to file.

Reading specific version

Now, let’s see the times required to read a specific version from each file.

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    vtimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        vtimes.append(read_version(filename, n))
    plt.plot(num_transactions, vtimes, '*-')

plt.xticks(num_transactions)
plt.title(f"Time (in sec) to read random version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

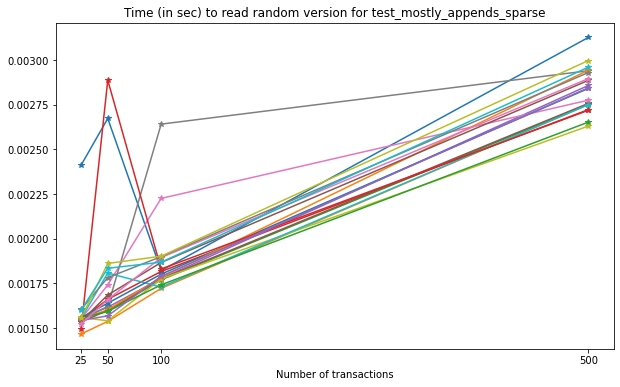
In this case, we can see a very clear increase in the time required to read versions from the file as the number of transactions increases. Again, this can be explained in part by the size of the datasets being read from file, as they grow in size with each new transaction.

Reading first version vs. reading latest version

Looking at the times required to read the first version and the latest version of the files, we get the following results.

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    ftimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ftimes.append(read_first(filename))
    plt.plot(num_transactions, ftimes, '*-')

plt.xticks(num_transactions)
plt.title(f"Time (in sec) to read first version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

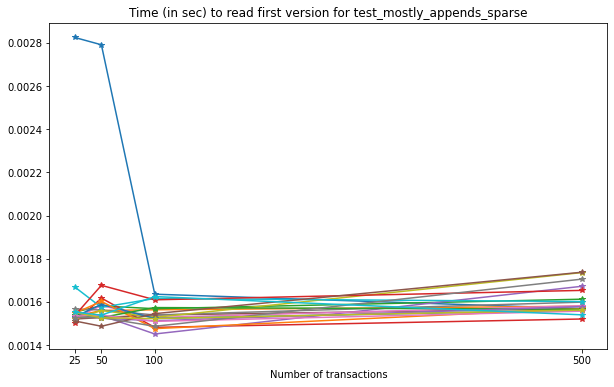
In this case, there is no significant increase in the time required to read the first version of the file as the number of transactions increases.

For the latest version, the results are as follows.

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))

notimes = []
for i in range(4):
    n = num_transactions[i]
    filename = f"{testname}_{n}_{exponent}_{compression}_no_versions.h5"
    notimes.append(read_no_versions(filename))
plt.plot(num_transactions, notimes, 'ko-', ms=6)
plt.legend(["No versions"], loc="upper left")

for _ in range(20):
    ltimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ltimes.append(read_last(filename))
    plt.plot(num_transactions, ltimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read latest version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

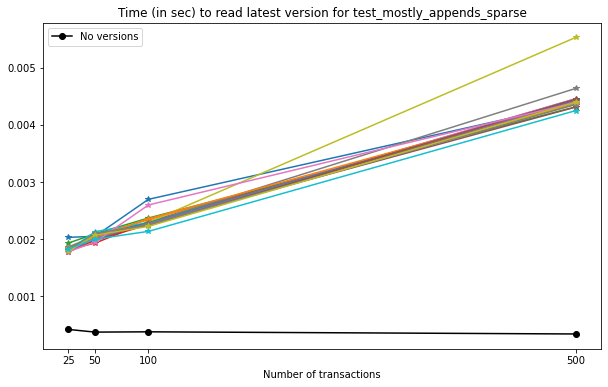
Note that here we can see the impact of storing all versions of the growing datasets on the VersionedHDF5File. While the unversioned file can be read in constant time, irrespective of the number of transactions commited, the versioned file suffers a slight drop in read performance (for 500 transactions, this amounts to an average difference of ~10x in seconds.)

Test 3: Small Fraction Changes (Sparse)

testname = "test_small_fraction_changes_sparse"

Reading in sequential mode

Once again, we only consider

compression = "None"
exponent = 14

Reading all versions in a file sequentially gives the following result.

rtimes = []
num_transactions = [50, 100, 500, 1000, 5000]
for n in num_transactions:
    filename = f"{testname}_{n}_{exponent}_{compression}.h5"
    rtimes.append(read_times(filename))

fig = plt.figure(figsize=(10,6))

plt.plot(num_transactions, rtimes, 'o-')
selected = [0, 3, 4]
plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Sequential read time (in sec) for {testname}")
plt.xlabel("Number of transactions")
plt.show()

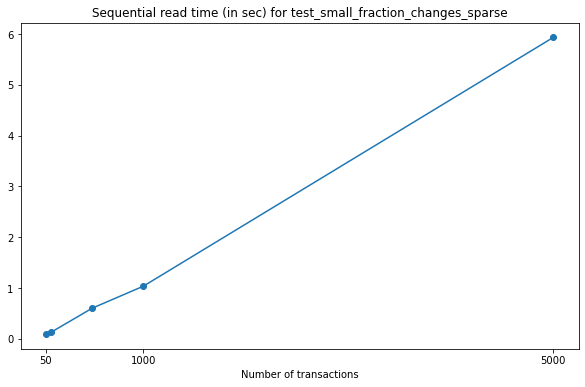
In this test, the sequential read times grow linearly with respect to the number of transactions commited to file.

Reading specific version

The times required to read a specific version from each file are similarly slightly affected by the number of existing versions in the file, as can be seen below.

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    vtimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        vtimes.append(read_version(filename, n))
    plt.plot(num_transactions, vtimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read random version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

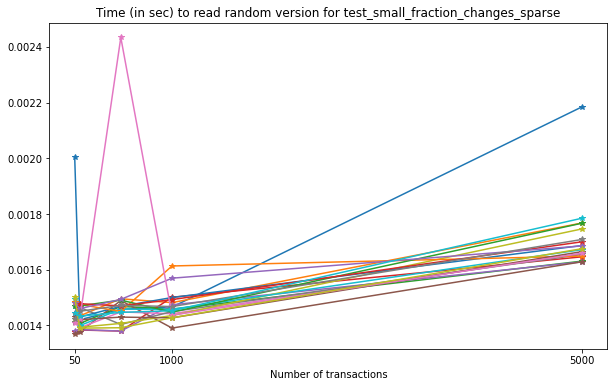
In this test, we can see there is again a slight increase in the time required to read a given version from each file as the number of transactions grows, similar to what we observe in test_large_fraction_changes_sparse.

Reading first version vs. reading latest version

Reading the first version from each file results in the following:

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    ftimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ftimes.append(read_first(filename))
    plt.plot(num_transactions, ftimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read first version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

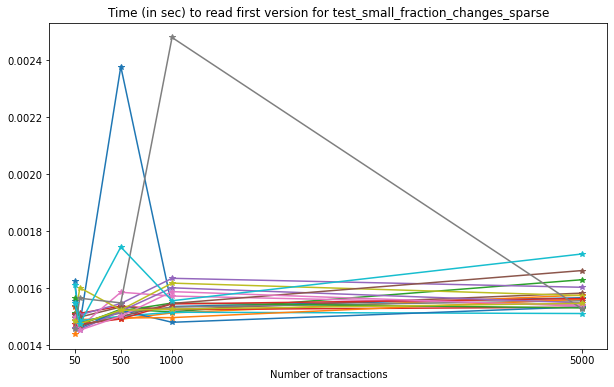
Comparing reading the latest version from a Versioned HDF5 file with an unversioned file (black line in the plot) results in the following:

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

notimes = []
for i in range(5):
    n = num_transactions[i]
    filename = f"{testname}_{n}_{exponent}_{compression}_no_versions.h5"
    notimes.append(read_no_versions(filename))
plt.plot(num_transactions, notimes, 'ko-', ms=6)
plt.legend(["No versions"], loc="upper left")

for _ in range(20):
    ltimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ltimes.append(read_last(filename))
    plt.plot(num_transactions, ltimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read latest version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

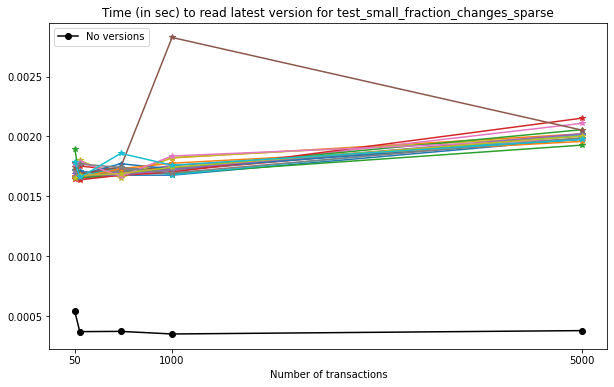
In this case, we can see that:

• reading the latest version is not as performant as reading an unversioned file;

• the time required to read the latest version from a Versioned HDF5 file increases modestly with the number of versions stored in the file;

• these results are similar to the ones obtained in test_large_fraction_changes_sparse.

Test 4: Large Fraction Changes (Sparse) - Constant Size

testname = "test_large_fraction_constant_sparse"

Once more,

compression = "None"
exponent = 14

Reading in sequential mode

Reading all versions from each file sequentially gives the following.

rtimes = []
num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

for n in num_transactions:
    filename = f"{testname}_{n}_{exponent}_{compression}.h5"
    rtimes.append(read_times(filename))

plt.plot(num_transactions, rtimes, 'o-')
selected = [0, 2, 3, 4]
plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Sequential read time (in sec) for {testname}")
plt.xlabel("Number of transactions")
plt.show()

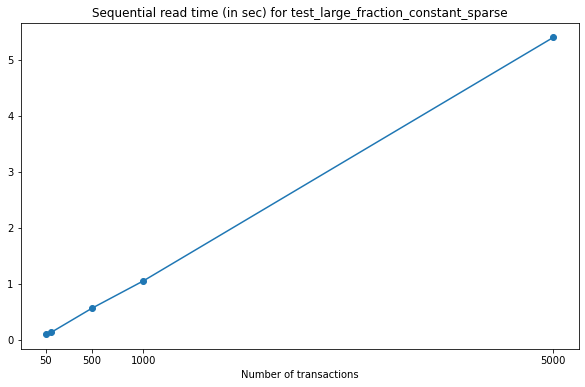
Again, the time required to read all versions in each file grows linearly with the number of transactions stored in each file.

Reading specific version

The times required to read a specific version from each file are similarly unnaffected by the number of existing versions in the file.

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    vtimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        vtimes.append(read_version(filename, n))
    plt.plot(num_transactions, vtimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read random version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

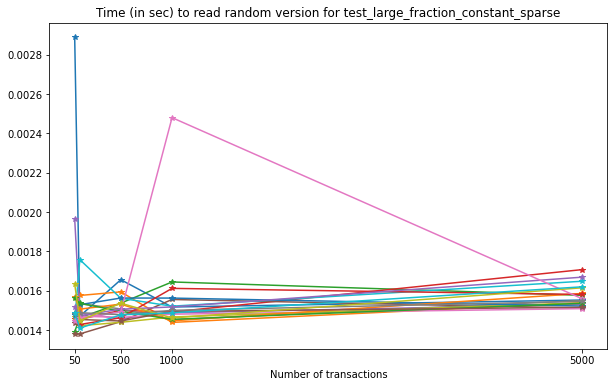
From this test, we can see that reading an arbitrary version from the file is only very slightly affected by the number of versions in the file.

Reading first version vs. reading latest version

Finally, let’s read the first version of each file.

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

for _ in range(20):
    ftimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ftimes.append(read_first(filename))
    plt.plot(num_transactions, ftimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read first version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

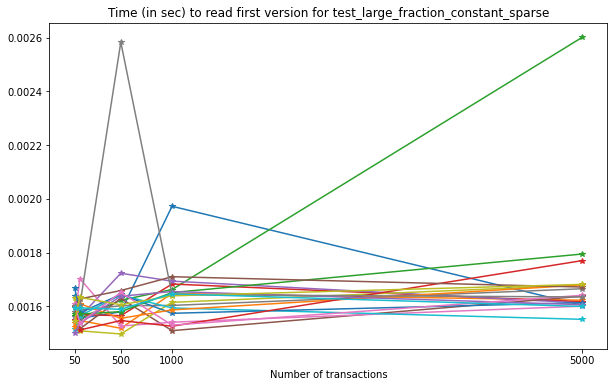
Comparing versioned and unversioned files for the latest version results in the following:

num_transactions = [50, 100, 500, 1000, 5000]

fig = plt.figure(figsize=(10,6))

notimes = []
for i in range(5):
    n = num_transactions[i]
    filename = f"{testname}_{n}_{exponent}_{compression}_no_versions.h5"
    notimes.append(read_no_versions(filename))
plt.plot(num_transactions, notimes, 'ko-', ms=6)
plt.legend(["No versions"], loc="upper left")

for _ in range(50):
    ltimes = []
    for i in range(5):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ltimes.append(read_last(filename))
    plt.plot(num_transactions, ltimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read latest version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

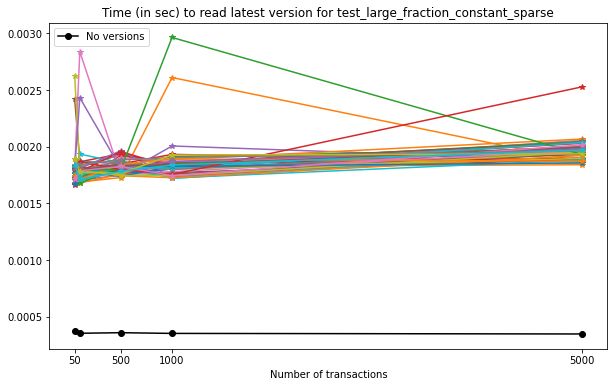
In this case, we can see that:

• reading the latest version is not as performant as reading an unversioned file;

• the time required to read the latest version from a Versioned HDF5 file increases very modestly with the number of versions stored in the file.

Test 5: Mostly appends (Dense)

Note that this test includes a two-dimensional dataset.

testname = "test_mostly_appends_dense"

Since this is a two-dimensional dataset, we have observed that a chunk size like the one used in previous examples will generate very large files, and will show a poor performance overall. In this case, we have chosen a chunk size of \(2^8\) as a sensible value for the current tests.

compression = "None"
exponent = 8

Reading in sequential mode

When we read all versions in sequential mode for this test, the results are as follows.

rtimes = []
num_transactions = [25, 50, 100, 500]
for n in num_transactions:
    filename = f"{testname}_{n}_{exponent}_None.h5"
    rtimes.append(read_times(filename))

fig = plt.figure(figsize=(10,6))

plt.plot(num_transactions, rtimes, 'o-')
selected = [0, 1, 2, 3]
plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Sequential read time (in sec) for {testname}")
plt.xlabel("Number of transactions")
plt.show()

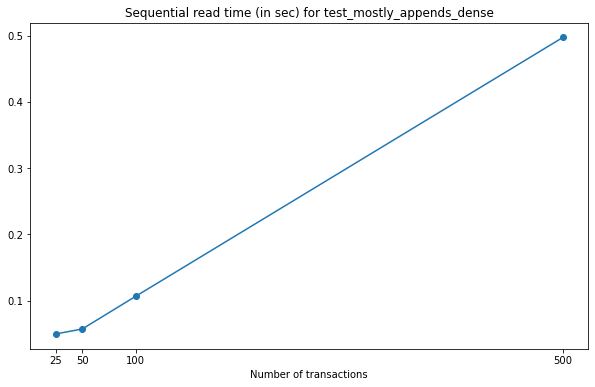
Note that this behaviour is not directly comparable to test_mostly_appends_sparse, as we have used a different chunk size and the dataset contains two-dimensional data. In this case, the increase in the time needed to read the dataset is close to linear.

Reading specific version

Now, let’s see the times required to read a specific version from each file.

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))
for _ in range(20):
    vtimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        vtimes.append(read_version(filename, n))
    plt.plot(num_transactions, vtimes, '*-')

plt.xticks(num_transactions)
plt.title(f"Time (in sec) to read random version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

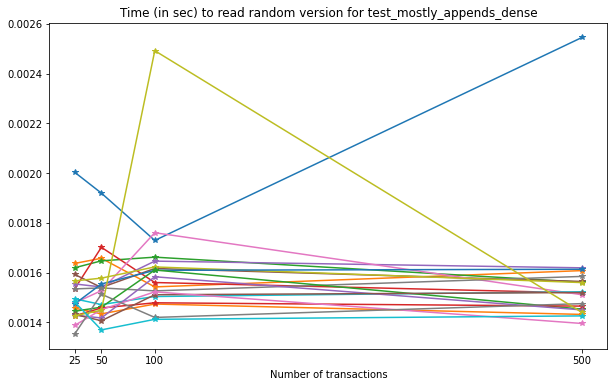
For this case, there is no marked increase in the time required to read a specific version from the file with respect to the number of versions.

Reading first version vs. reading latest version

Reading the first version of each of these files results in the following.

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))
for _ in range(20):
    ftimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ftimes.append(read_first(filename))
    plt.plot(num_transactions, ftimes, '*-')

plt.xticks(num_transactions)
plt.title(f"Time (in sec) to read first version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

For the latest version, once again comparing with the unversioned file, we have the following results:

num_transactions = [25, 50, 100, 500]

fig = plt.figure(figsize=(10,6))

notimes = []
for i in range(4):
    n = num_transactions[i]
    filename = f"{testname}_{n}_{exponent}_{compression}_no_versions.h5"
    notimes.append(read_no_versions(filename))

plt.plot(num_transactions, notimes, 'ko-', ms=6)
plt.legend(["No versions"], loc="upper left")

for _ in range(20):
    ltimes = []
    for i in range(4):
        n = num_transactions[i]
        filename = f"{testname}_{n}_{exponent}_{compression}.h5"
        ltimes.append(read_last(filename))
    plt.plot(num_transactions, ltimes, '*-')

plt.xticks(np.array(num_transactions)[selected])
plt.title(f"Time (in sec) to read latest version for {testname}")
plt.xlabel("Number of transactions")
plt.show()

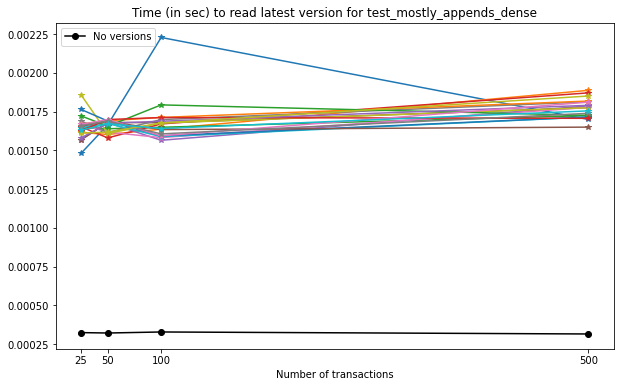
In this case:

• There is no marked increase in the time required to read the latest version with respect to the number of versions in each file;

• Reading a versioned file is, on average, 5x slower than reading a file containing only the last version of the data.

Summary

• test_mostly_appends_sparse shows the worst performance, with a considerable increase in the times required to read the latest version with respect to the number of transactions in the file.

• test_large_fraction_changes_sparse, test_small_fraction_changes_sparse and test_large_fraction_constant_sparse show better results in those same tests.

• test_mostly_appends_dense includes a two-dimensional dataset, and this does not seem to hinder performance of the versioning beyond what is observed in other one-dimensional tests.

• The same behaviour can be observed when reading a specific version from each file.

• This reflects what we observe in file sizes and can be partially explained by the increase in the dimension of the arrays which are stored at each version.

• Reading the first version is, in all tests, seemingly unaffected by the number of transactions involved in the file.